Big O Notation - what is it, where it lives, what it eats

Postado em 10/06/2025 Atualizado 16/06/2025

Por Daniel Mesquita

10 min de leitura

I had an interview today, and after almost two hours of a good conversation about some key concepts of algorthims and good practices of coding, there is some topics that I would like to share with you. Maybe you’re a skilled software engineer, this may be sound as obvious to you but my main public is entry-level engineers and students.

The first topic I would like to talk about it is the Big O Notation. It is something that you might no heard about if you started to learn from online course on youtube (or even the paid ones) that focuses only on languages and frameworks.

DSA in general and other things that people love to say on social media that “you will never use in real life” are things the people usually take for granted.

Yes, you may never use it like you use in plataforms like Leetcode, Hackerrank etc. But when you are creating your own algorithms, these concepts are deeply related with the quality of your code.

What is a good code? Two things:

Readable
Scalable

Readable code is a clean and clear code that other people can understand.

But in this I’m focusing on performance, so I’m talking about scalability. And here is the Big O enters.

Good code

When we’re creating an algorithm to allow our aplication to do something, we are setting instructions so the machine can execute what we want.

When you’re a baking a cake, you have many ways to do it. The instructions should work well with our kitchen and tools so we can bake the cake.

And there is a good way and a bad way to bake a cake. I’m not a chef, but I know that we can make a mess in our kitchen just to bake a cake that might no be so tasty or pretty.

The use of ingredients and tools, the choice of each step will follow the next, everything you choose, will impact in the final result. Maybe you will take longer than it should, maybe your cake will be disgusting, maybe you will blow up your kitchen…

The same logic we can use in our code. Computer need to work with our instructions to provide some sort of output. There are many ways to give these instructions.

Big O and “in my machine works better”

When I did my first readings about big O and how to measure code performance, I insisted to think about how long the code will take to finish its execution.

But the time is relative. I don’t want to talk about Einstein theories. Time is relative because the time an algorithm will take to run depends on the machine processing power, how many applications are running at the same time, which programming language is used, if it is running in a cloud server… A lot of variables.

The things changed when I started to think about number of operations.

Let’s say you want to find an item looping through an array.

  
public class FindItemInArray {
    public static void main(String[] args) {
        String[] items = {"apple", "banana", "orange", "grape"};
        String target = "orange";


        for (int i = 0; i < items.length; i++) {
            if (items[i].equals(target)) {
                System.out.println("Found " + target + " at index " + i);
            }
        }
    }
}

If you hit run in this code in your machine, will run in a different time than mine. And that’s irrelevant. Everytime you run this code it will be different, all factors I said before will impact in your runtime.

The important thing is how many data we have to deal and how we decide to deal with it.

Is there a way for us to measure what is good code and bad code? As the number of items in the array increases, it will slow down more and more.

Big O notations is the “language” we use for talking about how long an algorithm takes to run. We can compare two algorithms to measure which one is better than the other when it comes to scale.

How to measure?

We can’t measure in simple time. When we grow bigger and bigger, how much the algorithm slow down? As an array increases it sizes, how many more operations do we need to do to achieve its goal?

Big O notation describes the upper limit of an algorithm’s performance in relation to the input size. It allows us to express how the runtime or space requirements grow as the input size increases.

Common Big O notations include:

O(1): Constant time — does not change with input size.
O(log n): Logarithmic time — grows slowly as input increases.
O(n): Linear time — grows directly with input size.
O(n log n): Linearithmic time — common in efficient sorting algorithms.
O(n^2): Quadratic time — grows quickly, often found in nested loops.
O(2^n): Exponential time — grows very quickly, impractical for large inputs.

Considering the code I showed in the last session, each fruit we add to the array, we will increase the number of the operations happening in the loop. So we have a clear case of O(n).

What happens if we have a function like this?

  
public class FindItemInArray {
    public static void main(String[] args) {
        String[] items = {"apple", "banana", "orange", "grape"};
        System.out.println("Found " + items[0]);
    }
}    

What would happen here if we add more items?

We’re always grabbing the first item. This is O(1), the number operations is 1, no matter how big the array is. Is a constant time.

How to calculate?

Calculate Big O notation doesn’t require complex math. Let’s get back to the first example:

  
public class FindItemInArray {
    public static void main(String[] args) {
        String[] items = {"apple", "banana", "orange", "grape"}; // O(1)
        String target = "orange"; //O(1)


        for (int i = 0; i < items.length; i++) { //O(n)
            if (items[i].equals(target)) { //O(1)
                System.out.println("Found " + target + " at index " + i);
            }
        }
    }
}

See the comments? Considering each step in the method, we can set different notations. But there are rules to make our lives easier:

Worst Case: We always consider the worst case scenario when calculating Big O. This means we look at the maximum number of operations that could occur. When we’re talking about scalability, we can’t assume that things will always work perfectly. For example, in the loop, if the item is not found, we will iterate through all items, which gives us O(n) in the worst case.
Drop Constants: We ignore constant factors because they do not significantly affect the growth rate as input size increases. For example, O(2n) is simplified to O(n).

  
public class FindItemInArray {
    public static void main(String[] args) {
        String[] items = {"apple", "banana", "orange", "grape"}; // O(1)
        String target = "orange"; // O(1)

        for (int i = 0; i < items.length; i++) { // O(n)
            if (items[i].equals(target)) { // O(1)
                System.out.println("Found " + target + " at index " + i);
            }
        }
    }
}

In this case, we can say that the time complexity is O(n) because the loop iterates through each item in the array, and the constant factors (like the number of items) do not change the overall growth rate.

Different terms for inputs:
- If you have nested loops, you multiply the complexities. For example, if you have two nested loops, each iterating through n items, the complexity is O(n^2).
- If you have multiple independent operations, you add their complexities. For example, if you have one operation with O(n) and another with O(m), the total complexity is O(n + m).
Drop Non Dominants Terms:
- When you have multiple terms, focus on the one that grows the fastest as input size increases. For example, O(n^2 + n) simplifies to O(n^2) because n^2 grows faster than n as n becomes large.

Considering these rules, we can have a clear understanding of how to calculate Big O notation and how to apply it in our code.

Why does it matter?

When we’re dealing with small data sets, the performance of our code might not be a big deal. But as the data grows, the performance can become a bottleneck. We tend to think only about the current state. But when we’re building applications, we need to think about the future. How will our code perform when the data grows? How will it scale?

When we understand Big O notation, we can make better decisions about our algorithms and data structures. We can choose the right approach for the problem at hand, ensuring that our code remains efficient and scalable.

How can I use it in my daily work?

You can apply Big O notation in your daily work by:

Analyzing the performance of your algorithms and data structures.
Identifying potential bottlenecks in your code.
Choosing the right algorithms and data structures based on their time and space complexities.
Refactoring your code to improve its performance.

For example, if you find that a certain algorithm has a time complexity of O(n^2) and is causing performance issues, you might consider using a more efficient algorithm with a time complexity of O(n log n) or O(n). Let’s see in next example how we can improve the performance of our code using Big O notation.

  
import java.util.HashMap;
public class FindItemInArray {
    public static void main(String[] args) {
        String[] items = {"apple", "banana", "orange", "grape"};
        String target = "orange";

        // Using a HashMap to improve performance
        HashMap<String, Integer> itemMap = new HashMap<>();
        for (int i = 0; i < items.length; i++) {
            itemMap.put(items[i], i);
        }

        Integer index = itemMap.get(target);
        if (index != null) {
            System.out.println("Found " + target + " at index " + index);
        } else {
            System.out.println(target + " not found");
        }
    }
}

In this example, we use a HashMap to store the items and their indices. This allows us to achieve O(1) time complexity for lookups, significantly improving performance compared to the O(n) complexity of the previous linear search.

As you can see in the image below, it is a good reference to have in mind when you’re thinking about performance and scalability of your code.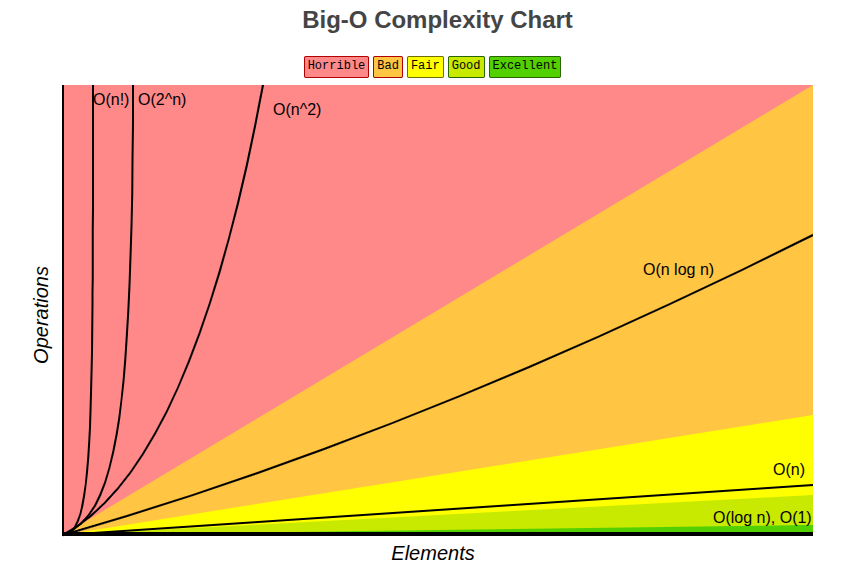

Big O Notation Recap

Big O notation is a way to describe the performance of an algorithm in terms of its time and space complexity. It helps us understand how an algorithm will scale with increasing input sizes and allows us to compare different algorithms based on their efficiency.

It is essential for writing efficient and scalable code, especially when dealing with large datasets or complex algorithms. By understanding Big O notation, we can make informed decisions about the algorithms and data structures we use in our applications.

In this post I’m not talking about memory usage, this is a topic for another post. But it is important to note that Big O notation can also be applied to space complexity, which refers to the amount of memory an algorithm uses as the input size increases.

This post is part of the things I like to share when I’m studying or learning something new. I try to keep it simple and clear, so you can understand the concepts without getting lost in technical jargon. If you have any questions or suggestions for future topics, feel free to reach out!